我们会因为高中时不同的教学水平和假期缺失一些高数中所需的高中数学知识,因此有了本文。
本文仅针对个人使用,不一定覆盖大多数人的情况,可以跳过。
0.1 函数
粗略来讲,函数就是在定义域内按对应法则能够将任意实数变换成另一个唯一确定的数。
隐函数
形如 \(y^3+2*y+x^2-x^4=0\) 的
一元三次方程,x 与 y 的关系隐藏于方程之中。
通常不使用普通的 \(f(x)\) 表示,而使用 \(F(x, y) = 0\)。
参数方程
给出下列函数: \[ \begin{align} y = \sin(t) \\ x = t^3+t \\ \end{align} \]
t 为自变量,x, y 为因变量,此时也是一个 y 关于 x 的函数。
我们可以得到如下图像:

输入 t 能够获得无数个 \((x, y)\) 的结果,这是一种由参数方程定义的函数。
0.2 三角函数与反三角函数
基本公式

反三角函数
反三角函数顾名思义,是三角函数的反函数。 即由对应的正余弦值得到对应的角度,但显然一个正余弦值可以对于多个角度,因此对于不同的反三角函数都有相对应的人为规定的取值范围。
反正弦
求其反函数即为 \(y = \sin(x)\) 关于 \(y = x\) 对称后得到的图像。但显然,我们所得到的图像并不是一个函数。
因此,我们只取对称后的部分函数。由于该函数是 \(y = \sin(x)\) 的反函数,因此原函数的值域即为反函数的定义域。其值域为 \([-\frac{\pi}{2}, \frac{\pi}{2}]\),定义域为 \([-1, 1]\),单调递增,为奇函数。
以下为反正弦函数 \(y = \arcsin(x)\) 的图像。
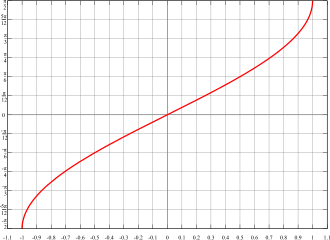
反余弦
与上面类似,反余弦作为余弦的反函数,推导思路与上面相同。
其值域为 \([0, \pi]\),定义域为 \([-1, 1]\),为单调递减函数,非奇非偶。
以下为反余弦函数 \(y = \arccos(x)\) 的图像。

反正切
值域 \((-\frac{\pi}{2}, \frac{\pi}{2})\),定义域 \((-\infty, \infty)\),单调递增,为奇函数。
以下为反正切函数 \(y = \arctan(x)\) 的图像。
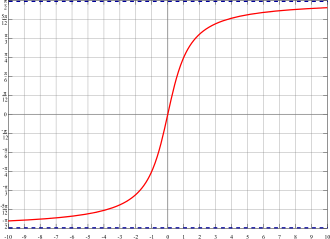
反余切
定义域为 \(R\),值域 \((0, \pi)\),单调递减,非奇非偶。
以下为反余切函数 \(y = arccot(x)\) 的图像。

正割
\(y = \sec(x) = \frac{1}{\cos(x)}\), \(\cos(x) ≠ 0\)
定义域:\(x \neq k\pi+\frac{\pi}{2}, k \in Z\)
值域:\((-\infty, -1]\cup[1, + \infty)\)
奇偶性:偶函数

余割
\(y = \csc(x) = \frac{1}{\sin(x)}, \sin(x)≠0\)
定义域:\(x \neq k\pi, k \in Z\)
值域:\((-\infty, -1]\cup[1, +\infty]\)
奇偶性:奇函数

0.3 多项式除法
在高中阶段,我们有时会遇到高次方程,但并没有很好的方法去解决它们。
多项式除法即用一个同次或低次的不等式去除另一个多项式,并且方便计算。其相除规则与整数相似。
给出以下除式:\(\frac{x^3+3x^2+3x+1}{x+1}\)
在相除时,通常需要由高次至低次排列,在缺项时补足一个 0。例如 \(x^3+x^2+0x+5\),补足 \(x\) 位。
我们首先观察 \(x + 1\) 与 \(x^3 + 3x^2\)。我们可以通过相乘使得 \(x+1\) 的最高次与后式相同,然后将相乘后的式子与后式直接相减,即 \((x^3+3x^2) - (x^3+x^2) = 2x^2\),将得到的 \(2x^2\) 与下一次位置相加,依此类推。
最终得到 \(\frac{x^3+3x^2+3x+1}{x+1} = (x+1)(x^2+2x+1)\)。
但并不是所有多项式都能整除。与除法相似,多项式除法中也存在着余数,一般地,我们会直接将余数加在后面,例如 \((x+2)(x^2+2x+4)+3\) (3 为余数)。
因式分解
在进行多项式除法时,决定除数是什么十分重要。
给出以下多项式:\(x^3-3x^2+4\)。
通常,我们通过试根得到除数。
例如,直接代入 \(x=1\),得到 \(1-3+4=2\)
代入 \(x=-1\),得到 \(-1-3+4=0\)
因此它存在一个可用的因式,为 \(x+1\)。
一般地,当满足 \(f(n) = 0\) 时,得到的可除因式即为 \(x-n\)。
0.4 有理分式拆分
有理分式拆分在高等数学的积分中被使用。有理分式的定义是分子及分母都是多项式的分式,例如 \(\frac{1}{(x+1)(x+2)}\)。
我们的目的是将相乘项变为相加减,利于求单独项的积分。
在分母已完成因式分解之后,可以尝试如下步骤拆分。
将相乘项直接拆开,如下所示
\(\frac{1}{x+1}\) 与 \(\frac{1}{x+2}\)
推断出右侧式子的正负
如此处我们可以先尝试推断右侧为 \(-\frac{1}{x+2}\),当拆分式子中存在分母中 \(x\) 存在系数的情况,则在对应式子中分母设为该系数。 然后通分得到 \(\frac{x+2-(x+1)}{(x+1)(x+2)} = \frac{1}{(x+1)(x+2)}\),即原式。
根据推导后式子与拆分后的式子比较,并通过相乘除的方式使二者一致。
如此处可直接得到 \(\frac{1}{x+1} - \frac{1}{x+2}\) 。 若分子并非 1,而是其他数字,通过相乘除转换。如得到 2 就在拆分后式子乘上 \(\frac{1}{2}\)。
我们可以得到:
\(\frac{1}{(x+a)(x+b)} = (\frac{1}{x+a} - \frac{1}{x+b})\times\frac{1}{b-a}=\frac{x+b-(x+a)}{(x+a)(x+b)}\)。
假分式
给出以下分式:\(\frac{2x^2-x+4}{x^2+3x+2}\),其分子次数与分母一样高,有一层伪装,因此诸如此类的分式被称为假分式,我们要通过配凑、因式分解等方式将其化为真分式。
例如 \(\frac{2x^2-x+4}{x^2+3x+2} = \frac{2(x^2+3x+2)-7x}{x^2+3x+2} = 2 -7\frac{x}{(x+1)(x+2)}\)
单独取出 \(\frac{x}{(x+1)(x+2)}\),进行因式分解。
与上面不同的是,我们得到了分子不为整数的分式。此时需要使用待定系数法:
\(\frac{x}{(x+1)(x+2)} = \frac{A}{x+1} + \frac{B}{x+2} = \frac{Ax+2A+Bx+B}{(x+1)(x+2)}\)
得到 \((A+B)x+2A+B=x+0\)
有 \[ \begin{align} A+B = 1 \\ 2A+B = 0 \\ \end{align} \] 得出 A=-1,B=2。最终代入回上式,得到拆分后的式子。
高次分式分解
给出以下式子:\(\frac{1}{(1+2x)(1+x^2)}\)
类推上述方法,为了保证分式中最高次为二次,拆分为 \(\frac{A}{1+2x}+\frac{Bx+C}{1+x^2}\)。
如上述步骤,进行通分并计算得到 \(A\) 与 \(B\) 的值。
0.5 复合函数求导
给出以下式子:\(y=f(u), u=g(x)\)。
链式法则: \(\frac{dy}{dx}=\frac{dy}{du}\times\frac{du}{dx}\),在复合函数的层数足够多的情况下,显现出链式求导,因此称为链式法则。
例:\(y=ln(\sin(x))\),求 \(\frac{dy}{dx}\)。
\(y=ln(u), u=\sin(x)\) => \(\frac{dy}{dx}=\frac{dy}{du}\times\frac{du}{dx} = \frac{1}{u}\times\cos(x)=\frac{1}{\sin(x)}\times\cos(x)=\cot(x)。\)
洋葱法则
如看洋葱一般,由外层看向内层,观察函数的构成。
例 \(y=e^{\sin x}\),求 \(\frac{dy}{dx}\)。
=> \(y'=e^{sin x} \times (\sin x)'=e^{\sin x} \times \cos x\)
一个更复杂的例子:求导 \(y=ln(\sin(e^{\sqrt x}))\)。
=> \(y' = \frac{1}{sin^(e^{\sqrt x})} \times \cos(e^{\sqrt x}) \times e^{\sqrt x} \times \frac{1}{2} \times \frac{1}{\sqrt x}\)
由外层求导逐步求导至内层
0.6 极坐标系
用于二重积分与三重积分之中。与我们所熟知的直角坐标系不同,坐标系由原点出发,利用 \((x, y)\) ,向 x 轴和 y 轴分别移动找点。极坐标则是通过转动 x, y 轴,由原点出发作一条射线找点。由两个参数决定:从 x 轴的正方向逆时针转动的角度 (\(\theta\))、该点到极点的距离(\(\rho\))。
极坐标系的原点称为极点,坐标轴称为极轴。极轴只沿 x 轴的正方向延伸,是一条射线。
同样存在单位长度。存在 $ $,\(0 \leq \theta < 2\pi\) (实际做题不一定,可以取负值)。
极坐标更多被用于表示平面内的线或面,而非坐标轴单纯的点。例如圆、圆面、圆环等。
半圆面

如图所示,这样的一个半圆面存在 \(0 \leq \theta \leq \frac{\pi}2\),但 \(\rho \neq 2\)。
我们任意向外做一条射线与圆面交于 M 点,转动\(\theta\),得到直角三角形。
这条射线与圆面所有的交点构成:\(0 \leq \rho \leq 2\cos\theta\)。